Linear-Feedback Shift 寄存器的 Galois 和 Fibonacci 多项式之间的转换

介绍

这个页面可以用一句话概括： 如果要将 LFSR的多项式从 Galois 形式转换为 Fibonacci 形式，请反转系数的顺序。

例如，这是 scramblers中经常使用的 LFSR 的图纸：

每个标有 D 的块是一个时钟周期（clock cycle）的时延（delay）。这 LFSR 作为 Galois 多项式的表示是：

G(x) = x¹⁶ + x⁵ + x⁴ + x³ + 1

请注意，多项式（3、4 和 5）中的指数反映了每个异或（XOR）左侧的时延 elements （delay elements）的数量。

同样的 LFSR 可以用 Fibonacci 的形式实现，如下图所示：

尽管这两幅图很相似，但箭头的方向是相反的。 LFSRs 的实现完全不同。

Fibonacci 多项式（或 feedback 多项式）是这样的：

F(x) = x¹⁶ + x¹³ + x¹² + x¹¹ + 1

多项式的阶数为 n=16，因此 G(x) 中的每 xⁱ 在 F(x) 中由 x^n-i表示。本页的其余部分说明了为什么这不是巧合。

有关 LFSRs的一般说明，请参阅有关此主题的Wikipedia 页面。

LFSR 和 digital 滤波器

digital 滤波器背后的理论（例如 FIRs 和 IIRs）通常应用于 field of complex numbers。但是，也可以将此理论应用于GF(2) ，即由两个数字组成的 finite field (Galois Field)： 0 和 1。有几点需要注意：

• 这 field 中的 plus operator 相当于一个异或。
• 所有乘法只涉及整数。实际上，乘以一个偶数就等于乘以0。同样，乘以一个奇数就等于乘以1。这个数是正数还是负数都没有关系。
• 由于这条乘法规则， plus 和 minus 意思相同。两者都可以替换为 ⊕ （即异或（XOR））。

digital 滤波器的基础理论只要求系统为 Linear time-invariant （LTI）即可。 LFSR 满足这些要求，因为异或是线性的，而 LFSR的行为是时不变的。

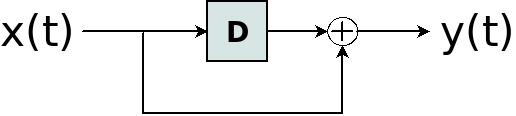
最有趣的结果是 z-transform 可以用来分析 LFSRs。例如，考虑这张图：

这可以用以下等式来描述：

y(t) = x(t) ⊕ x(t-1)

t 是一个表示时间的整数。

可以将其视为 FIR，并写出此等式的 z-transform ：

Y(z) = X(z) + X(z)z^-1=X(z) (1 + z^-1)

因此，“impulse response”可以像往常一样定义： H(z) = Y(z)/X(z)，或者简单地说：

H(z) = 1 + z^-1

但是如果我们一个接一个地放置两个这样的过滤器会怎样呢？这个过滤器的“impulse response”是什么？

digital 滤波器的理论有一个简单的答案：

H₂(z) = H(z)H(z) = (1 + z^-1)(1 + z^-1) = 1 + 2z^-1 + z^-2

回想一下，对于 GF(2)，与偶数的乘法就像与零的乘法。因此，

H₂(z) = 1 + 2z^-1 + z^-2 = 1 + 0z^-1 + z^-2=1 + z^-2

这对应于：

很难看出最后两张图中显示的过滤器是等价的。但是，当两个滤波器被馈入相同的 x(t)时，它们会产生相同的 y(t) 。所以过滤器是相同的，即使存储在第二个时延 element （delay element）中的值不同。

此示例显示了使用 z-transform （以及多项式的类似技术）分析逻辑滤波器（logic filters）的优势。

我应该提一下，通常使用符号 D 或 D^-1 而不是 z^-1。实际上，在 Galois 和 Fibonacci 多项式中使用 x 与 z^-1具有相同的含义。所有这些符号都表示时延。

Galois LFSR

为了找到 Fibonacci 表示，我将从查看 Galois LFSR开始。

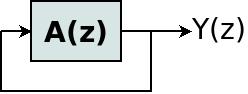
从上方考虑 Galois LFSR 的绘图。时延 lines （delay lines）和 taps 这一行可以看作是一 FIR 过滤器，我将其表示为 A(z)。因此， Galois LFSR 等同于：

由于 feedback， Y(z) 的等式为：

Y(z) = Y(z)A(z)

那么这 FIR的参数和 Galois 的多项式有什么关系呢？让我们写出 Galois 多项式的一般形式：

G(x) = xⁿ + g_n-1x^n-1+ g_n-2x^n-2+…+ g₀

注意 g_n 没有出现在这个表达式中，以简化下面的数学计算。此外， g_n 始终等于 1。

G(x) 与 A(z) 的关系如下：

A(z) = g_n-1z^-1+g_n-2z^-2+…+g₁z^1-n+g₀z^-n

为什么这是正确的？让我们以上图中的 Galois LFSR 为例，展示此表达式的工作原理。

首先我们来看 g₅对应的异或。数字5表示在这个异或的左边有五个时延 elements （delay elements）。但 z 的指数取决于异或和 FIR的输出（output）之间的时延 elements 的数量。这些是异或右侧的时延 elements 。总共有16个时延 elements 。因此， g₅ 在 A(z) 中显示为 g₅z^-11。这与 g_n-iz^-i 模式匹配。

解释这一点的另一种方法是将 A(z) 视为 time domain中的 FIR 。这 FIR的输入是 x(t) ，它的输出是 y(t)：

y(t) = x(t–16) ⊕ x(t–13) ⊕ x(t–12) ⊕ x(t–11)

同样， t 是一个表示时间的整数。此表达式表示没有 feedback的 Galois LFSR 。这 FIR的 transfer 函数是：

A(z) = Y(z)/X(z) = z^-16 + z^-13 + z^-12 + z^-11

这与 A(z) 和 G(x) = x¹⁶ + x⁵ + x⁴ + x³ + 1的一般表达式一致。

相当于 Fibonacci

Fibonacci 形式的 LFSR 由以下多项式表示：

F(x) = f_nxⁿ+f_n-1x^n-1+…+f₁x + 1

注意 f₀ 没有出现在这个多项式中，因为它总是等于 1。这类似于 G(x)中没有出现 g_n 。

这个多项式的实现是：

y(t) = f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n)

因此， z transform 是：

Y(z) = f₁Y(z)z^-1+f₂Y(z)z^-2+…+f_nY(z)z^-n

让我们定义 B(z) 如下：

B(z) = f₁z^-1+f₂z^-2+…+f_nz^-n

因此Y(z) 可以写成：

Y(z) = Y(z)B(z)

回想一下上面的 Y(z) = Y(z)A(z)。因此，如果 LFSR 的 Fibonacci 形式与 Galois 多项式给出的 LFSR 表现相同，则它遵循 A(z) = B(z)。这也意味着：

f_i=g_n-i (i=1,2, … , n)

所以正如我一开始所说： 为了将 LFSR的多项式从 Galois 形式转换为 Fibonacci 形式，反转系数的顺序。

LFSR的 inverse 滤波器

再一次，这是 LFSR的 Fibonacci 实现：

y(t) = f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n)

但这个表达式也可以改写如下：

y(t) + f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n) = 0

（回想一下 + 和 – 在 GF(2)中是一样的）

因此， Fibonacci 多项式的系数还告诉我们如何对 y(t-i) 的值执行异或，以便始终获得零值。换句话说，这描述了一个有趣的 FIR。

最后一个表达式的 z transform 是：

Y(z) + f₁Y(z)z^-1+f₂Y(z)z^-2+…+f_nY(z)z^-n = 0

或者，等效地：

Y(z)(1+ f₁z^-1+f₂z^-2+…+f_nz^-n) = Y(z)H(z) = 0

当过滤器 H(z) 应用于 Y(z)时，Y(z)H(z) 是输出。而这个输出（output）为零。

因此 H(z) 是 FIR 滤波器的 transfer 函数。如果将 F(x)定义的 LFSR 的输出馈入此 FIR ，则输出将始终为零。从上面 B(z) 的定义来看，这 FIR的 transfer 函数是：

H(z) = 1 + f₁z^-1+f₂z^-2+…+f_nz^-n

或者在 time domain中，如果输入是 x(t) ，输出是 y(t)：

y(t) = x(t) ⊕ f₁x(t-1) ⊕ f₂x(t-2) ⊕ … ⊕ f_nx(t-n)

如果 x(t) 是由 F(x)定义的 LFSR 的输出，则对于所有 t， y(t) 为零。