01signal.com

logic design에서 timing 의 기본

中文 | 日本語 | 한국어 | English

이 페이지는 timing에 대한 일련의 페이지 에 속합니다.

이 페이지 정보

logic design의 몇 가지 기본 주제를 모른 채 timing을 올바르게 수행하는 것은 불가능합니다. 이 페이지에서는 나머지 페이지 시리즈의 기초가 되는 몇 가지 기본 개념에 대해 설명합니다.

아래에 쓰여진 모든 내용은 logic design에 대한 학술 과정에서 가르칩니다. 그러나 FPGAs 로 작업하는 모든 사람이 이러한 종류의 과정을 수강한 것은 아니며 그러한 과정을 수강한 사람들도 반드시 모든 것을 기억하는 것은 아닙니다. 이 페이지는 누락된 부분이 있는 경우 이를 채우기 위한 것입니다.

이 페이지에서 이미 알고 있는 부분은 건너뛰어도 되지만, 이 내용이 피상적일지라도 모든 내용을 읽는 것이 좋습니다. 이 페이지의 마지막 섹션은 이 시리즈의 다음 페이지를 이해하는 데 특히 중요합니다.

간단한 리뷰

timing와 관련된 개념에 들어가기 전에 logic design의 몇 가지 관련 용어를 빠르게 검토하겠습니다. 이러한 용어가 아직 알려지지 않은 경우 이 페이지를 계속하기 전에 해당 용어에 익숙해지는 것이 좋습니다.

먼저 combinatorial logic입니다. 이 용어는 logic gates와 같은 요소를 설명하는 데 사용됩니다. AND gate, OR gate, NOT gate등. 이러한 logic elements는 메모리가 없기 때문에 combinatorial logic 로 간주됩니다. 즉, 그들의 행동은 과거에 일어난 일에 의존하지 않습니다. 이러한 logic elements 의 output 값은 inputs값에만 의존합니다.

combinatorial logic 의 중요한 유형은 look-up table (LUT)입니다. 이것은 여러 inputs에 의존하는 모든 logic function을 구현하는 다목적 logic element입니다. LUT는 FPGA내부의 거의 모든 combinatorial logic 에 사용되기 때문에 중요합니다. FPGA 내부의 LUTs는 asynchronous ROMs 로 구현됩니다(예: clock이 없는 ROMs ). inputs는 LUT내부의 데이터를 address 로 처리합니다. output은 일반적으로 하나 또는 두 개의 bits로 구성됩니다.

inputs 에서 이러한 LUTs 까지의 개수는 시중의 거의 모든 FPGAs 에서 4 또는 6이 므로 각 LUT 의 메모리 셀 개수는 16 또는 64입니다.

다음으로 중요한 용어는 sequential logic입니다. 여기에는 작동을 위해 clock이 필요한 flip-flops, synchronous RAMs및 기타 여러 빌딩 블록이 포함됩니다. 이 모든 logic elements는 clock의 특정 변경에 대한 반응으로 활성화됩니다. 이러한 활동 순간 사이에 sequential elements는 inputs를 무시하고 내부 상태를 유지하며 outputs를 변경하지 않습니다.

예를 들어, positive edge triggered logic elements는 clock이 낮음에서 높음(예: rising clock edge)으로 변경될 때 활성화됩니다. 마찬가지로 negative edge triggered logic elements는 clock이 높음에서 낮음(예: falling clock edge)으로 변경될 때 활성화됩니다. 두 clock edges모두에서 활성화되는 logic elements 도 있지만 이러한 logic elements는 거의 I/O signals를 샘플링하거나 생산하는 데만 사용됩니다.

모든 sequential elements 에는 일종의 메모리가 있습니다. 이것은 clock edge가 도착할 때까지 output을 변경하지 않는다는 사실에서 즉각적인 결론입니다. 일부 sequential elements 에는 최소한의 메모리가 있으며, 이는 각 output에 정확히 하나의 bit 메모리입니다. 다른 sequential elements 에는 더 많은 메모리가 있습니다(예: shift registers 및 RAMs).

timing에 대해 논의하기 위해 두 가지 중요한 사실이 있습니다. input은 clock edge와 함께만 샘플링되고 output은 거의 clock edge의 결과로만 변경됩니다. 한 가지 예외가 있는데, 일부 sequential elements 에는 asynchronous reset input이 있습니다. 이 input이 활성화되면( logic element에 따라 높음 또는 낮음) sequential element 의 내부 상태는 clock와 관계없이 사전 정의된 값으로 즉시 변경됩니다. 결과적으로 이 요소의 일부 또는 전체 outputs 도 알려진 값으로 즉시 변경됩니다.

FPGA에서 일부 sequential elements 에는 asynchronous reset이 있고 다른 sequential elements 에는 없습니다. asynchronous reset은 FPGA의 거의 모든 sequential elements 에서 가능한 유일한 asynchronous input 입니다. 이것은 logic design 의 이론이 S-R flip-flop와 같이 여러 asynchronous inputs와 함께 여러 elements를 포함하는 경우에도 마찬가지입니다.

지금부터 flip-flops에 대해 이야기하겠습니다.

단순화를 위해 모든 sequential elements는 positive edge triggered flip-flops, 즉 clock의 rising edge 에 반응하는 flip-flops 라고 가정합니다. 즉, 여기서는 모든 sequential elements가 flip-flops로 표시됩니다. 이 flip-flops는 inputs 에 응답하고 clock이 낮음에서 높음으로 변경될 때만 outputs를 업데이트합니다.

이렇게 하면 timing을 이해하기가 더 쉽고 flip-flop 에 대한 논의는 다른 모든 sequential element로 쉽게 일반화됩니다.

Setup 및 hold

flip-flop이 올바르고 안정적으로 작동하도록 하려면 inputs가 안정적이어야 합니다(즉, 값이 변경되지 않아야 함). 이는 두 가지 timing requirements에 따른 것입니다.

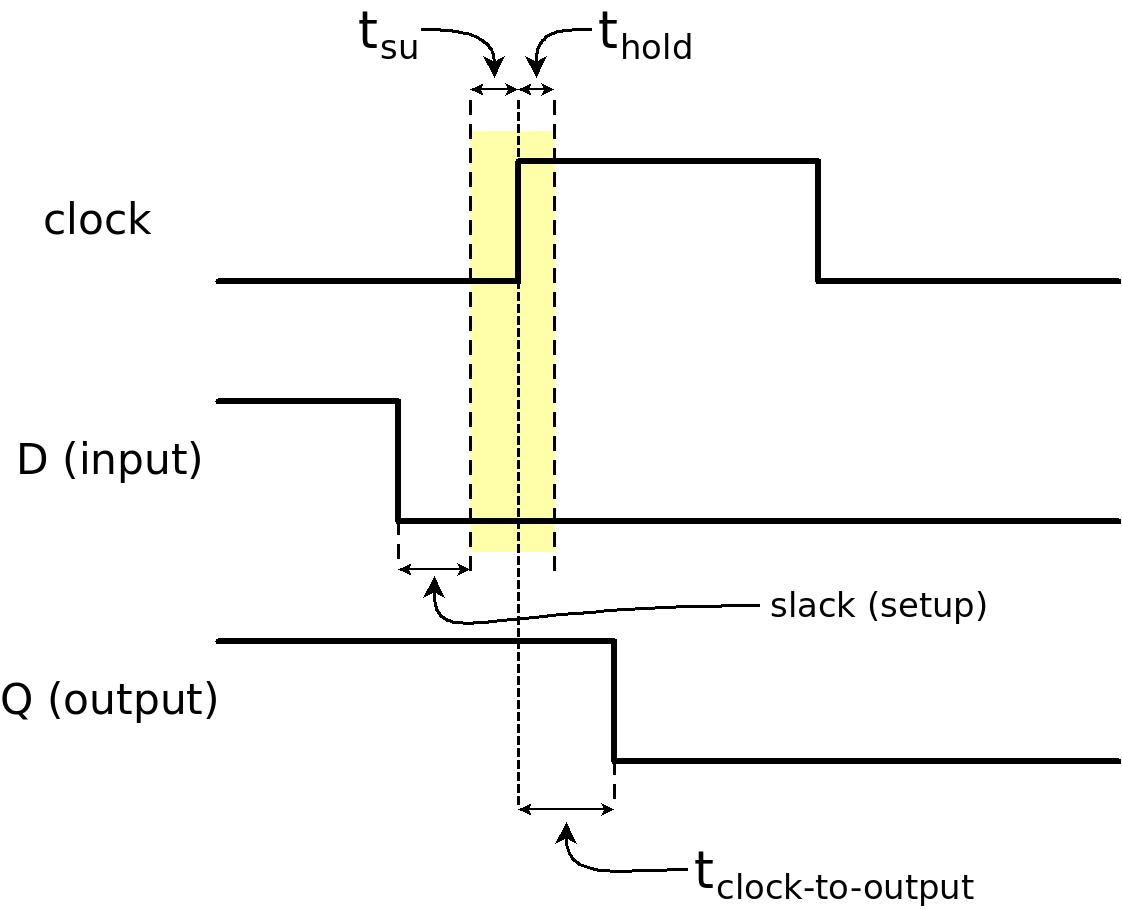
Timing diagram showing setup and hold times

위 그림은 tsu 및 thold의 의미를 보여줍니다. D input은 노란색으로 표시된 기간 내에서 값을 변경할 수 없습니다. 이 예에서 D는 합법적인 timing을 사용하여 높음에서 낮음으로 변경됩니다. 즉, 이 노란색 기간을 벗어납니다.

이 두 가지 timing parameters를 이해하는 한 가지 방법은 다음과 같습니다. input 에서 flip-flop 로의 변경이 clock edge와 정확히 함께 변경되는 경우 flip-flop이 해당 input을 높음 또는 낮음으로 처리할지 확실하지 않습니다. 무엇을 선택해야 할까요? clock edge 직전 또는 이후의 상태는?

그러면 input이 clock edge와 "정확히 함께" 변경되었다는 것이 무슨 의미인지 물어볼 수 있습니다. 얼마나 정확한가요? 두 개의 timing parameters, tsu 및 thold는 clock edge 에서 input의 값을 변경하는 것이 얼마나 안전한지 정의합니다. 이러한 매개변수는 모든 sequential elements 에 대해 동일한 의미로 정의됩니다.

이 timing requirement가 위반되면 그 결과는 clock edge 이후의 flip-flop 의 output이 무작위라는 것보다 훨씬 더 나쁠 수 있다는 점에 유의하는 것이 중요합니다. 그 이유는 두 가지입니다.

Clock-to-output

모든 sequential elements 에 대해 정의된 세 번째 timing parameter은 clock-to-output 시간으로, 여기에는 tcko, tco, tC_Q 등과 같은 몇 가지 공통 기호가 있습니다. 이 매개변수는 timing requirement가 아닙니다. 오히려 이 매개변수는 the sequential element 의 output (Q)가 언제 유효할지를 말합니다. 더 정확히 말하면, clock edge 이후 얼마 후에 output이 유효한지(위의 timing diagram 참조)를 말합니다.

실제로 이 문제에는 두 가지 매개변수가 있습니다.

대부분의 경우 최대 clock-to-output 만이 흥미롭기 때문에 이 매개변수가 datasheet 에 제공되면 거의 확실하게 최대값입니다.

flip-flop의 timing requirements (tsu 및 thold)가 위반되면 output이 언제 안정될지 보장할 수 없습니다. 이 경우 flip-flop이 잠시 동안 정의되지 않은 상태(metastability)에 머무를 가능성이 있으므로 최대 clock-to-output parameter은 의미가 없습니다.

tsu 및 thold는 음수가 될 수 있습니다.

위의 그림에서 양수 tsu 및 thold가 표시되더라도 이러한 매개변수 중 하나 또는 둘 다 음수 값을 가질 수 있습니다. 실제로 FPGAs 내부의 flip-flops는 매우 작은 음수를 사용하더라도 두 매개변수가 모두 음수인 경우가 많습니다.

예를 들어 음수 tsu는 clock edge가 도착했을 때 data가 안정적일 필요가 없음을 의미합니다. 오히려 data는 clock edge이후 에 안정적인 값에 도달했을 것입니다. 그러나 tsu는 clock edge이후에도 여전히 한계를 두고 있습니다.

마찬가지로 네거티브 thold를 사용하면 data가 clock edge보다 먼저 변경될 수 있습니다. 다시 한 번, 이것이 허용되기 전에는 여전히 제한이 있으며 이는 thold에 반영됩니다.

tsu 와 thold는 모두 음수일 수 있으므로 이론적으로 말도 안 되는 timing requirements를 정의할 수 있습니다. 예를 들어, thold가 tsu 에 의해 안정되기 전에 input이 변경되도록 허용한다면 그것은 말이 되지 않습니다. 실제 timing 사양의 경우 이런 일은 절대 일어나지 않을 것입니다. 사양은 input이 안정적이어야 하는 특정 기간을 정의해야 합니다. 그러한 기간이 없다면 flip-flop은 언제 input을 샘플링합니까?

clock-to-output parameter은 항상 긍정적입니다. flip-flop은 clock edge가 도착하기 전에 반응할 수 없습니다.

Propagation delay

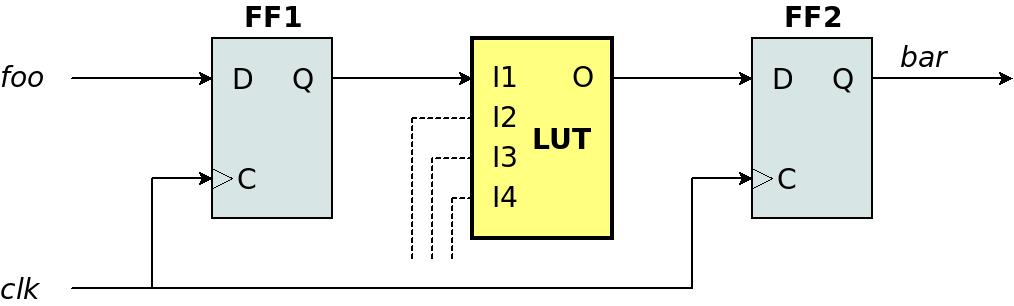
Two flip-flops connected through a LUT

위의 그림은 중간에 LUT가 있는 두 개의 flip-flops 사이의 간단한 연결을 보여줍니다. 단순화를 위해 LUT의 output이 I1에만 의존한다고 가정해 보겠습니다. 예를 들어 이 logic은 다음 Verilog 코드의 결과일 수 있으므로 LUT는 NOT gate를 구현합니다.

always @(posedge clk)
  begin
    foo_reg <= foo;   // FF1 = foo_reg
    bar <= !foo_reg;  // FF2 = bar
  end

두 flip-flops는 동일한 clock에 연결되어 있습니다. 이 clock의 최대 주파수는 얼마입니까?

이 질문에 답하기 위해 누락된 정보가 있습니다. FF1의 output이 안정적인 값을 갖는 순간부터 FF2의 input이 안정적인 값을 갖기까지 얼마나 걸립니까? 시간과 함께 tpd (propagation delay)로 표시합니다.

propagation delay 라는 용어는 항상 combinatorial logic의 특정 segment 와 관련이 있습니다. 관련된 segment를 명시적으로 정의하는 것이 중요합니다. 예를 들어, LUT의 I1 에서 동일한 LUT의 O 까지( input 에서 output까지) 시간을 propagation delay로 정의하는 것도 가능합니다. 이 delay은 아마도 이전의 tpd정의와 다를 것입니다.

특히 FPGA에서는 FF1 의 output 와 LUT의 input 사이에 routing delay이 있습니다. 따라서 실생활에서 FF1의 Q는 LUT의 I1와 동일한 지점이 아니며 signal이 이 두 지점 사이를 전파하는 데 시간이 걸립니다.

이러한 모호성 때문에 FPGAs의 경우 datasheets 에 tpd 기호가 표시되는 경우는 드뭅니다. 그리고 이러한 datasheets에서 propagation delay이 제공될 때 이 매개변수의 정확한 의미는 일반적으로 명시적으로 작성됩니다.

나중에 clock의 최대 주파수로 다시 돌아오겠습니다.

path

path에 대한 간결한 정의를 내리기는 어렵지만 우리는 이미 이에 대한 예를 보았습니다. 위에서 tpd를 FF1의 Q 와 FF2의 D사이의 propagation delay 로 정의했습니다. 이 tpd는 특정 시나리오와 관련이 있습니다. FF1이 값을 변경하고 업데이트된 값이 LUT에 도달한 후 LUT가 output을 변경하고 마지막으로 업데이트된 값이 FF2에 도달합니다. 이 일련의 이벤트는 하나의 signal (FF1의 output)만 변경하면 시작되고 다른 지점(FF2의 input)에서 signal이 안정될 때 끝납니다.

따라서 tpd는 FF1의 Q 에서 FF2의 D까지 path 의 propagation delay 로 정의됩니다. 간단히 말해서 FF1 에서 FF2로의 path 입니다.

path는 이 시퀀스의 시작부터 끝까지 delay을 발생시키는 모든 요소로 구성됩니다. path에는 두 가지 유형의 요소가 있습니다.

path 의 목적은 propagation delay을 계산하는 것입니다. 이 계산 결과가 사용되는 방법은 다음에 나와 있습니다.

종종 path는 하나의 flip-flop의 output이 변경되고 다른 flip-flop의 input 로 이어지는 특정 경로를 따르는 이론적 실험을 나타냅니다. 이 이론적 실험에서는 첫 번째 flip-flop 의 output이 변경될 때 가상의 스톱워치가 시작됩니다. 두 번째 flip-flop 의 input이 변경되면 이 스톱워치가 중지됩니다.

이 이론적 실험은 이 스톱워치가 표시하는 시간이 너무 긴지, 즉 tsu 에 대한 요구 사항을 위반했는지 여부에 대한 답을 찾는 데 도움이 됩니다. 두 번째 질문은 이 시간이 너무 짧아서 thold가 위반되었는지 여부입니다.

path 의 경로에는 배선과 combinatorial logic만 포함됩니다. 따라서 signal이 목적지에서 안정될 때까지 걸리는 시간은 path를 따라 combinatorial logic 및 routing 의 요소에만 의존합니다. 이 이론적 실험이 언제 이루어졌는지는 중요하지 않으며 결과는 항상 동일합니다.

실제 FPGA design에서 각 flip-flop 에는 일반적으로 input에 도달하는 많은 paths 와 output에서 시작하는 많은 paths가 있습니다. 사실 한 쌍의 flip-flops 사이에도 둘 이상의 path가 있을 수 있습니다. 그러나 timing 계산은 항상 하나의 flip-flop 만 output을 변경했으며 FPGA의 logic 에서 발생하는 모든 것은 해당 변경의 직접적인 결과라는 가정하에 이루어집니다. FPGA design 에서 계산되는 paths 의 수는 엄청날 수 있지만 이것은 물론 소프트웨어에 의해 자동으로 수행됩니다.

간단한 static timing analysis

데모를 위해 두 개의 flip-flops로 위 예제의 간단한 timing analysis를 만들겠습니다. timing constraints 에 대한 주제는 추후에 다루겠지만 당분간은 @clk 의 주파수가 250 MHz (4 ns)이고, logic 에 직접 연결되어 있다고 가정하자(즉, PLL없이 실제 design에서는 권장하지 않음) , 그러나 이것은 timing analysis를 단순화합니다 ). timing constraint ( SDC 스타일)는 다음과 같을 수 있습니다.

create_clock -period 4.000 -name clk [get_ports clk]

이 시리즈의 다음 페이지 에 실제 timing analysis 의 예가 나와 있지만, 그 분석은 정확하기 때문에 이해하기 어려운 많은 세부 사항을 포함하고 있습니다. 따라서 이것은 원리를 보여주는 간단한 분석입니다.

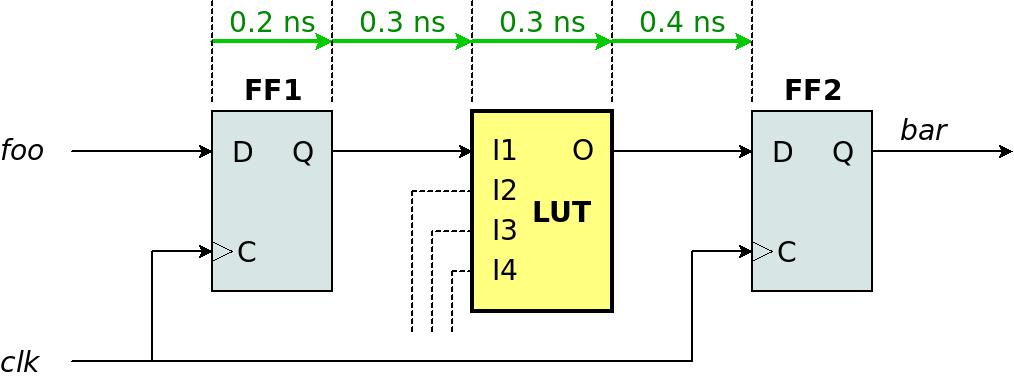
분석은 위에서 언급한 이론적 실험을 수행합니다. 가상의 스톱워치는 @clk의 rising edge와 함께 시작됩니다. 이것은 각 이벤트가 기여하는 (가상) delay 와 함께 일련의 이벤트입니다.

Timing delay of path with a LUT between two flip-flops

이 path 의 propagation delay (tpd)는 다음 모든 delays의 합계입니다. 0.2 + 0.3 + 0.3 + 0.4 = 1.2 ns. 예제를 위해 FF2의 tsu가 0.1 ns라고 가정합니다. 이는 FF2의 input (D)가 @clk의 다음 rising edge 이전에 안정적인 0.1 ns 여야 함을 의미합니다. 즉, 허용되는 최대 tpd는 4 - 0.1 = 3.9 ns입니다.

그러나 tpd는 1.2 ns일 뿐이므로 이 계산에 따르면 path는 큰 차이로 timing constraint를 달성합니다. 이 여백은 slack라고 하며 이 경우에는 3.9 - 1.2 = 2.7 ns입니다. 소프트웨어의 timing 계산에 이 숫자가 나타나면 도구가 timing constraints를 달성하는 데 어려움을 겪었는지 여부를 나타냅니다. slack이 0에 가까우면 소프트웨어가 path를 timing requirements에 맞게 만들기 위해 열심히 작업해야 함을 나타내는 경우가 많습니다.

propagation delay을 사용하면 이 path가 timing을 달성할 수 있는 @clk 의 최대 주파수를 계산할 수도 있습니다. tpd는 1.2 ns가 고 tsu 요구 사항은 다음 rising edge가 나중에 0.1 ns 에 도착할 수 있음을 의미합니다. 즉, rising edges사이에 최소한 1.3 ns가 있어야 합니다. 이는 약 769 MHz의 주파수를 의미합니다. 이것은 매우 높은 주파수이지만 path 에는 단일 LUT만 포함되어 있기 때문에 현실적인 결과입니다. 실제 logic은 일반적으로 실제보다 더 복잡하기 때문에 실제 주파수가 훨씬 낮은 경우가 많습니다.

실제 static timing analysis는 이 계산을 정확하게 하지만, 그것은 이야기의 일부일 뿐입니다. 여기서 계산된 path는 실제 계산에서는 data path 라고 합니다. 그러나 실제 static timing analysis는 또한 clock edge가 정확히 같은 시간에 두 flip-flops 에 도착하지 않는다는 점도 고려합니다. 이는 clock buffer 에서 이 flip-flops 각각까지의 delay이 약간 다르기 때문입니다. 이 delays 사이의 차이를 clock skew라고 합니다. 또한 clock jitter때문에 각 clock edge 사이의 시간이 정확히 같지 않습니다. clock 의 이러한 문제는 다음 페이지 에 표시된 것처럼 정확한 계산을 더 복잡하게 만듭니다.

Recovery 및 Removal

flip-flop 에 asynchronous reset input이 있는 경우( 정말 원 하십니까?) 이 input이 비활성화되는 시기에 대한 요구 사항이 있습니다. flip-flop은 어쨌든 알려진 상태로 변경되기 때문에 reset이 언제 활성화되는지는 중요하지 않습니다.

그러나 reset이 비활성화되면 flip-flop이 clock에 민감해지기 시작합니다. reset 의 비활성화가 clock edge근처에서 발생하면 flip-flop이 이에 응답해야 하는지 확실하지 않습니다. tsetup 및 thold와 마찬가지로 reset은 clock edge주변의 기간 동안 안정적이어야 합니다. 또는 더 구체적으로:

이러한 정의는 tsetup 및 thold의 정의와 유사합니다. 그것은 우연이 아닙니다. recovery time은 setup time의 특별한 종류입니다. timing analysis 도 같은 방식으로 수행됩니다. 유일한 차이점은 setup time이 data signal의 가치와 상관없이 관련이 있다는 것입니다. 반대로 asynchronous reset signal이 활성으로 변경되면 recovery time은 적용되지 않습니다. removal time 와 hold time 의 관계는 동일합니다.

이러한 유사성 때문에 Recovery 및 Removal은 이 언급 이상으로 논의되지 않습니다. 또한 위의 내용은 asynchronous reset뿐만 아니라 모든 asynchronous inputs에도 적용됩니다.

RTL paradigm 및 timing

위에 표시된 두 개의 flip-flops가 있는 예는 간단하지만 RTL paradigm로 생성된 모든 logic을 나타냅니다. 각 path는 flip-flop 에서 시작하여 동일한 clock (또는 related clock)가 있는 flip-flop 에서 끝납니다. path 자체는 combinatorial logic 와 routing로 구성됩니다. 이 예에서 combinatorial logic은 하나의 LUT가 지만 path의 여러 logic elements 와 실질적인 차이는 없습니다. 구조는 동일합니다.

RTL paradigm이 중요한 이유는 이 방법을 사용할 때 거의 모든 data paths가 이와 같은 간단한 구조를 갖기 때문입니다. 그리고 logic design 에 있는 paths 의 수는 종종 엄청나기 때문에 timing analysis 의 단순성은 실수를 방지하는 데 도움이 됩니다. 무엇보다 timing analysis가 특정 패턴을 가지고 있다는 사실은 timing report를 읽고 말이 되는지 물어볼 수 있게 합니다.

따라서 가능한 한 모든 것이 sequential element 에서 시작하여 sequential element에서 끝나야 합니다. 이것은 Verilog 코드를 작성할 때와 logic의 구조를 일반적으로 계획할 때 유용한 지침입니다.

이것으로 timing constraints의 이론에 대한 간략한 소개를 마칩니다. clock period constraint 및 관련 timing reports는 다음 페이지 에서 설명합니다.

이 페이지는 영어에서 자동으로 번역됩니다. 불분명한 사항이 있으면 원본 페이지를 참조하십시오.
Copyright © 2021-2024. All rights reserved. (b4b9813f)