Linear-Feedback Shift Registerの Galois 多項式と Fibonacci 多項式の間の変換

序章

このページは、次の 1 つの文に要約できます。 LFSRの多項式を Galois 形式から Fibonacci 形式に変換する場合は、係数の順序を逆にします。

たとえば、これは scramblersでよく使用される LFSR の図面です。

D でマークされた各ブロックは、1 つの clock cycleの delay です。 Galois 多項式としてのこの LFSR の表現は次のとおりです。

G(x) = x¹⁶ + x⁵ + x⁴ + x³ + 1

多項式の指数 (3、4、および 5) は、各 XORの左側にある delay elements の数を反映していることに注意してください。

次の図に示すように、同じ LFSR を Fibonacci 形式で実装できます。

これらの 2 つの図は類似していますが、矢印の方向が逆になっています。 LFSRs の実装は完全に異なります。

Fibonacci 多項式 (または feedback 多項式) は次のとおりです。

F(x) = x¹⁶ + x¹³ + x¹² + x¹¹ + 1

多項式の次数は n=16であるため、 G(x) 内の各 xⁱ は x^n-iによって F(x) で表されます。このページの残りの部分では、これが偶然ではない理由を示しています。

LFSRsに関する一般的な説明については、このトピックのWikipedia ページを参照してください。

LFSR および digital filters

digital filters の背後にある理論 (たとえば、 FIRs および IIRs) は通常、 field of complex numbersに適用されます。ただし、この理論をGF(2)に適用することもできます。これは、2 つの数値で構成される finite field (Galois Field) です。 0 と 1。注意すべき点がいくつかあります。

• この field の plus operator は XORと同等です。
• すべての乗算には整数のみが含まれます。実際には、偶数を掛けることは 0 を掛けることと同じです。同様に、奇数を掛けることは 1 を掛けることと同じです。この数が正か負かは問題ではありません。
• この掛け算のルールにより、 plus と minus は同じ意味になります。どちらも ⊕ (つまり XOR) に置き換えることができます。

digital filters の基本理論は、システムが Linear time-invariant (LTI) であることのみを必要とします。 XOR は線形であり、 LFSRの動作は時不変であるため、 LFSR はこれらの要件を満たしています。

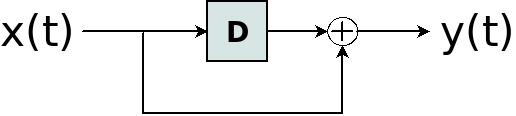
最も興味深い結果は、 z-transform を使用して LFSRsを分析できることです。たとえば、次の図を考えてみましょう。

これは、次の式で説明できます。

y(t) = x(t) ⊕ x(t-1)

t は時間を表す整数です。

これを FIRとして扱い、この式の z-transform を書くことができます。

Y(z) = X(z) + X(z)z^-1=X(z) (1 + z^-1)

したがって、「impulse response」は通常どおり定義できます。 H(z) = Y(z)/X(z)、または単に:

H(z) = 1 + z^-1

しかし、これらのフィルターを 2 つ並べるとどうなるでしょうか。このフィルターの「impulse response」とは？

digital filters の理論には簡単な答えがあります。

H₂(z) = H(z)H(z) = (1 + z^-1)(1 + z^-1) = 1 + 2z^-1 + z^-2

GF(2)では、偶数の乗算はゼロの乗算に似ていることを思い出してください。によると、

H₂(z) = 1 + 2z^-1 + z^-2 = 1 + 0z^-1 + z^-2=1 + z^-2

これに対応します：

最後の 2 つの図に示されているフィルターが同等であることを確認するのは簡単ではありません。しかし、どちらのフィルターも、同じ x(t)を供給すると、同じ y(t) を生成します。したがって、2 番目の delay element に格納されている値は同じではありませんが、フィルターは同じです。

この例では、 z-transform (および多項式を使用した同様の手法) を使用して logic filtersを解析する利点を示します。

z^-1の代わりに D または D^-1 のシンボルがよく使用されることに注意してください。実際、 Galois および Fibonacci 多項式での x の使用は、 z^-1と同じ意味を持ちます。これらの記号はすべて delayを意味します。

Galois LFSR

Fibonacci 表現を見つけるために、 Galois LFSRを調べることから始めます。

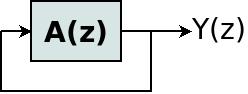
上から見た Galois LFSR の図を考えてみましょう。 delay lines と taps の行は FIR フィルターと見なすことができ、これを A(z)とします。したがって、 Galois LFSR はこれと同等です。

feedbackのため、 Y(z) の式は次のとおりです。

Y(z) = Y(z)A(z)

では、この FIRのパラメータと Galois 多項式の間の接続は何ですか? Galois 多項式の一般的な形式を書きましょう。

G(x) = xⁿ + g_n-1x^n-1+ g_n-2x^n-2+…+ g₀

以下の数学を単純化するために、この式には g_n が表示されないことに注意してください。また、 g_n は常に 1と等しくなります。

G(x) と A(z) の関係は次のとおりです。

A(z) = g_n-1z^-1+g_n-2z^-2+…+g₁z^1-n+g₀z^-n

なぜこれが正しいのですか？上の図から Galois LFSR を取り出して、この式がどのように機能するかを示しましょう。

まずは g₅に対応する XOR から見ていきましょう。 5という数字は、この XORの左側に5台の delay elements があることを意味します。ただし、 z の指数は、 XOR と FIRの outputの間の delay elements の数に依存します。これらは、 XORの右側にある delay elements です。 delay elements は全部で16台。したがって、 g₅ は g₅z^-11として A(z) に表示されます。これは g_n-iz^-i パターンと一致します。

これを説明する別の方法は、 A(z) を time domainの FIR と見なすことです。この FIRの input は x(t) であり、その output は y(t)です。

y(t) = x(t–16) ⊕ x(t–13) ⊕ x(t–12) ⊕ x(t–11)

繰り返しますが、 t は時間を表す整数です。この表現は、 feedbackを除いた Galois LFSR を表します。この FIRの transfer function は次のとおりです。

A(z) = Y(z)/X(z) = z^-16 + z^-13 + z^-12 + z^-11

これは、 A(z) と G(x) = x¹⁶ + x⁵ + x⁴ + x³ + 1の一般的な表現と一致しています。

Fibonacci 相当品

Fibonacci 形式の LFSR は、次の多項式で表されます。

F(x) = f_nxⁿ+f_n-1x^n-1+…+f₁x + 1

f₀ は常に 1に等しいため、この多項式には表示されないことに注意してください。これは、 G(x)に表示されない g_n に似ています。

この多項式の実装は次のとおりです。

y(t) = f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n)

したがって、 z transform は次のとおりです。

Y(z) = f₁Y(z)z^-1+f₂Y(z)z^-2+…+f_nY(z)z^-n

B(z) を次のように定義しましょう。

B(z) = f₁z^-1+f₂z^-2+…+f_nz^-n

したがって、Y(z) は次のように記述できます。

Y(z) = Y(z)B(z)

その Y(z) = Y(z)A(z)の上から思い出してください。したがって、 LFSR の Fibonacci 形式が Galois 多項式によって与えられる LFSR と同じように動作する場合、 A(z) = B(z)に従います。これは、次のことも意味します。

f_i=g_n-i (i=1,2, … , n)

だから私は最初から言ったように： LFSRの多項式を Galois 形式から Fibonacci 形式に変換するには、係数の順序を逆にします。

LFSRの inverse filter

繰り返しますが、これは LFSRの Fibonacci 実装です。

y(t) = f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n)

しかし、この式は次のように書き直すこともできます。

y(t) + f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n) = 0

( + と – は GF(2)で同じであることを思い出してください)

したがって、 Fibonacci 多項式の係数は、常に値ゼロを取得するために、 y(t-i) の値に対して XOR を実行する方法も教えてくれます。つまり、これは興味深い FIRを表しています。

最後の式の z transform は次のとおりです。

Y(z) + f₁Y(z)z^-1+f₂Y(z)z^-2+…+f_nY(z)z^-n = 0

または、同等に:

Y(z)(1+ f₁z^-1+f₂z^-2+…+f_nz^-n) = Y(z)H(z) = 0

Y(z)H(z) は、 Y(z)にフィルター H(z) を適用した場合の output です。そしてこの output はゼロ。

したがって、 H(z) は FIR filterの transfer function です。この FIR に、 F(x)で定義された LFSR の output をフィードすると、 output は常にゼロになります。上記の B(z) の定義から、この FIRの transfer function は次のようになります。

H(z) = 1 + f₁z^-1+f₂z^-2+…+f_nz^-n

または、 time domainで、 input が x(t) で、 output が y(t)の場合:

y(t) = x(t) ⊕ f₁x(t-1) ⊕ f₂x(t-2) ⊕ … ⊕ f_nx(t-n)

x(t) が F(x)によって定義される LFSR の output である場合、 y(t) はすべての tに対してゼロです。